project 2

The disparity between the rapidly increasing computing performance and the slow increase in storage and I/O bandwidth of supercomputers necessitates data compression, where data produced by simulations are compressed in situ and decompressed in situ and post hoc for analysis and exploration. However, most of today’s lossy compressors (e.g., ZFP, FPZIP, SZ, etc.) provide global error bounds on the decompressed data, which do not guarantee the preservation of topological features essential to scientific discoveries. We worked on developing advanced data reduction techniques and software that preserve topological features in data for in situ and post hoc analysis and visualization at extreme scales.

Left: Eliminate topological false cases with iterations. Right: 3D visualization of original and decompressed data with different parameter settings. Images from [VIS23b].

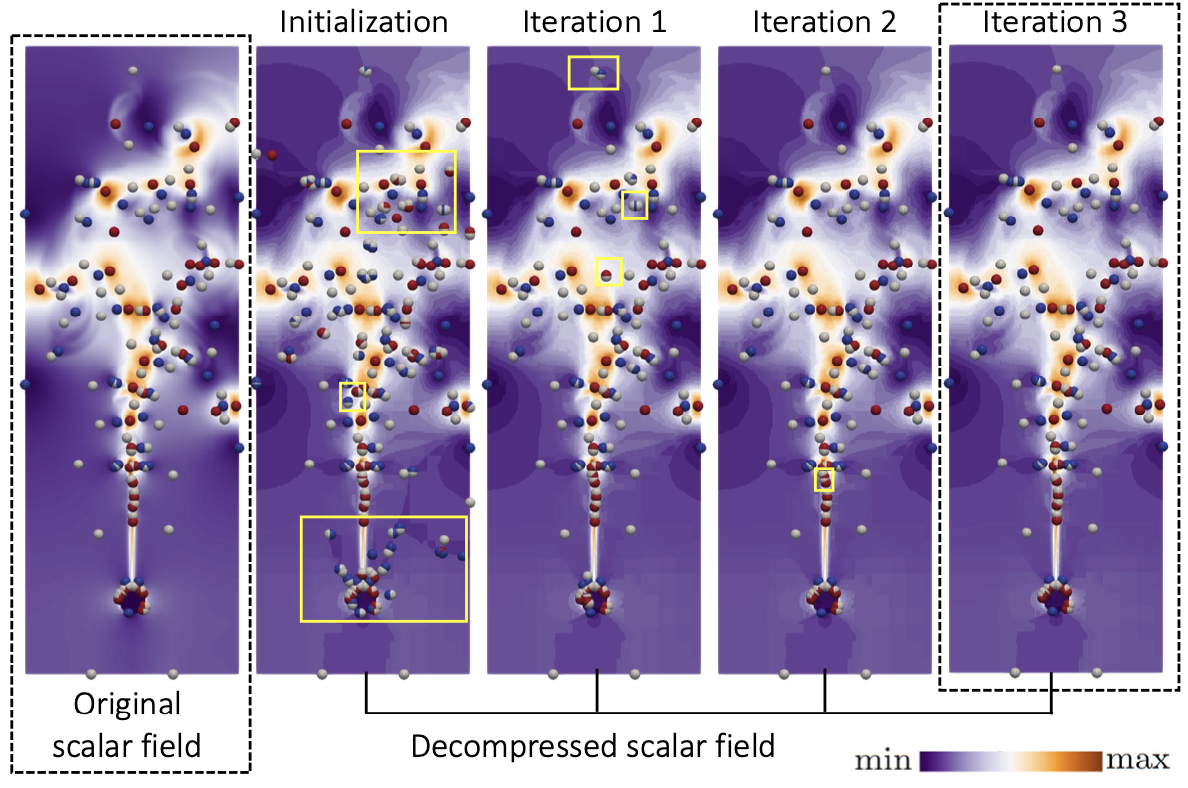
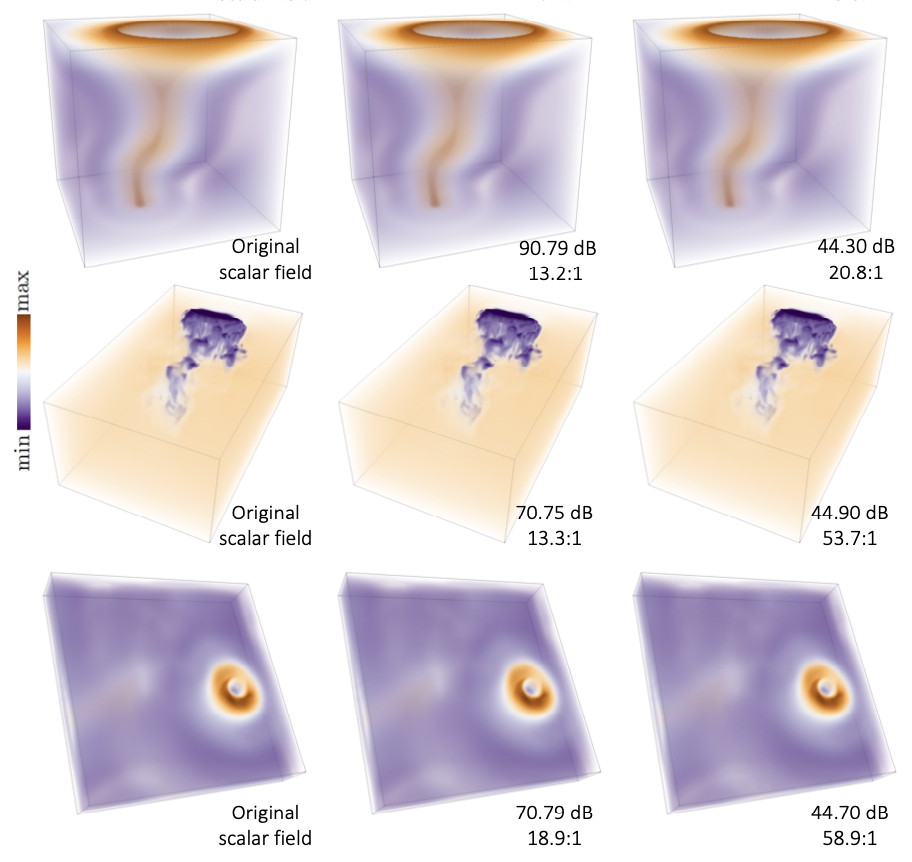
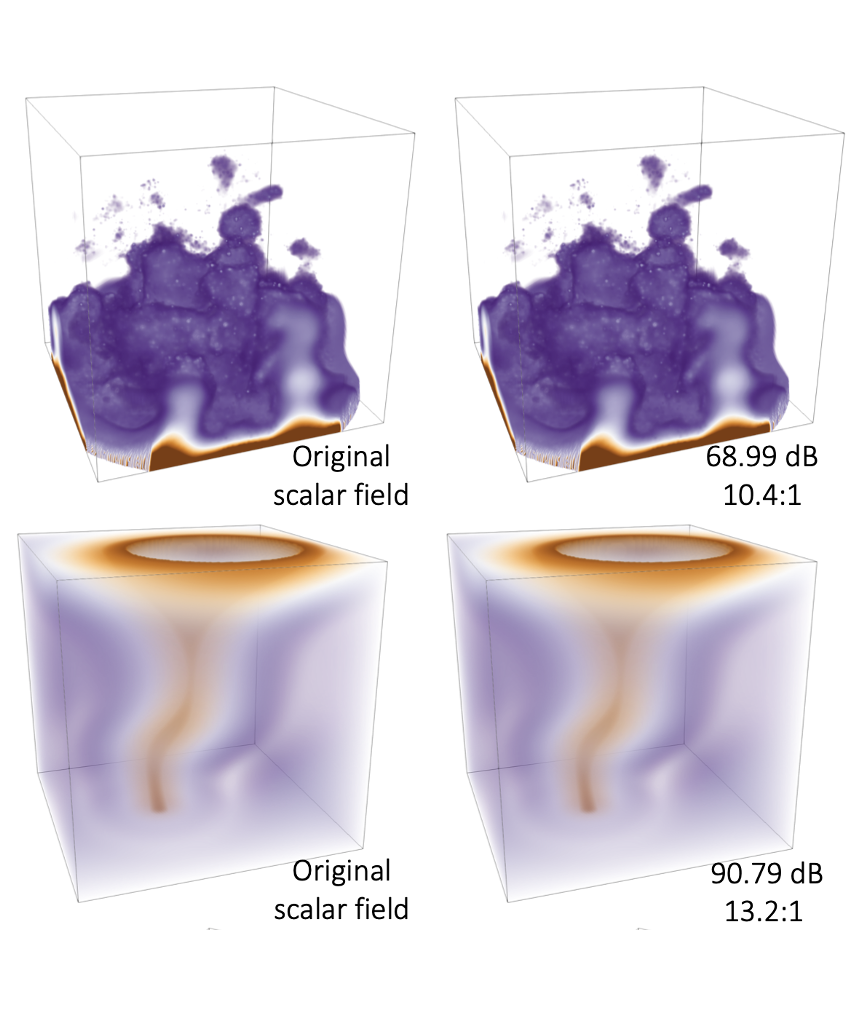
We designed and led the development of TopoSZ [VIS23b], an error-bounded lossy compression method that preserves the topological features in 2D and 3D scalar fields. The main idea is to derive topological constraints from contour-tree-induced segmentation from the data domain and incorporate such constraints with a customized error-controlled quantization strategy from the SZ compressor. Our method allows users to control the pointwise error and the loss of topological features during compression.

Left: Homology-preserving dimensionality reduction using manifold landmarking: original point clouds, Isomap embeddings, random landmark Isomap embeddings, and homological landmark Isomap embeddings. Right: original point cloud, Isomap embeddings without tearing, with partial tearing and with the optimal tearing, respectively. Images from [VDS18].

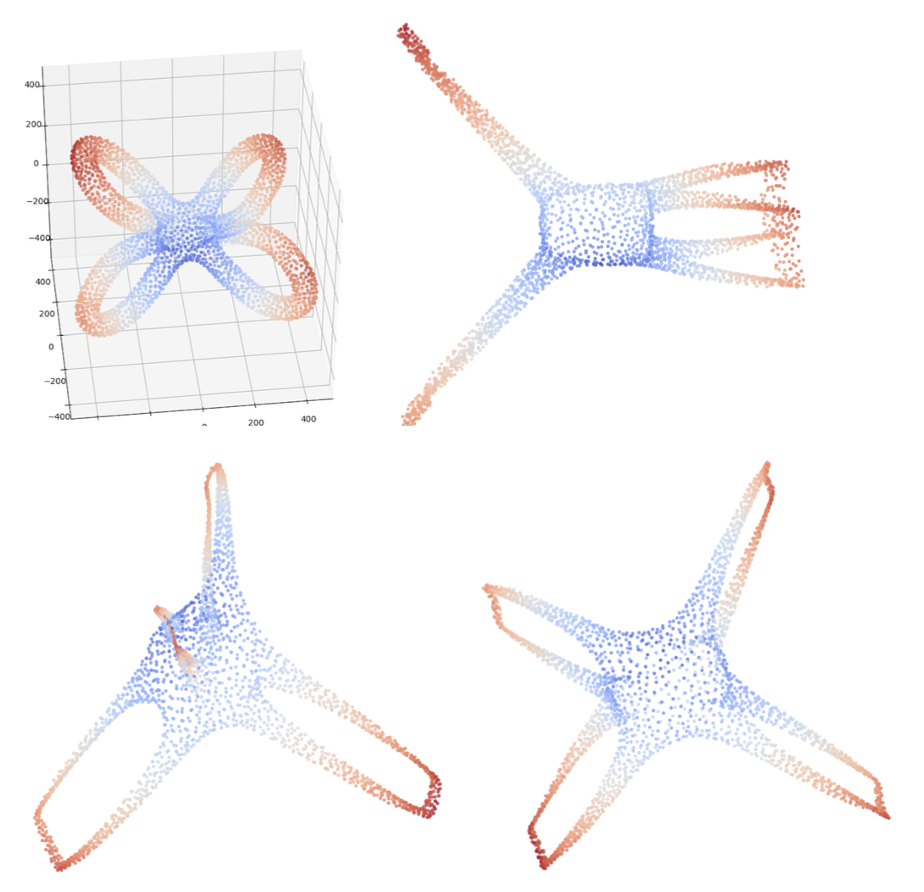
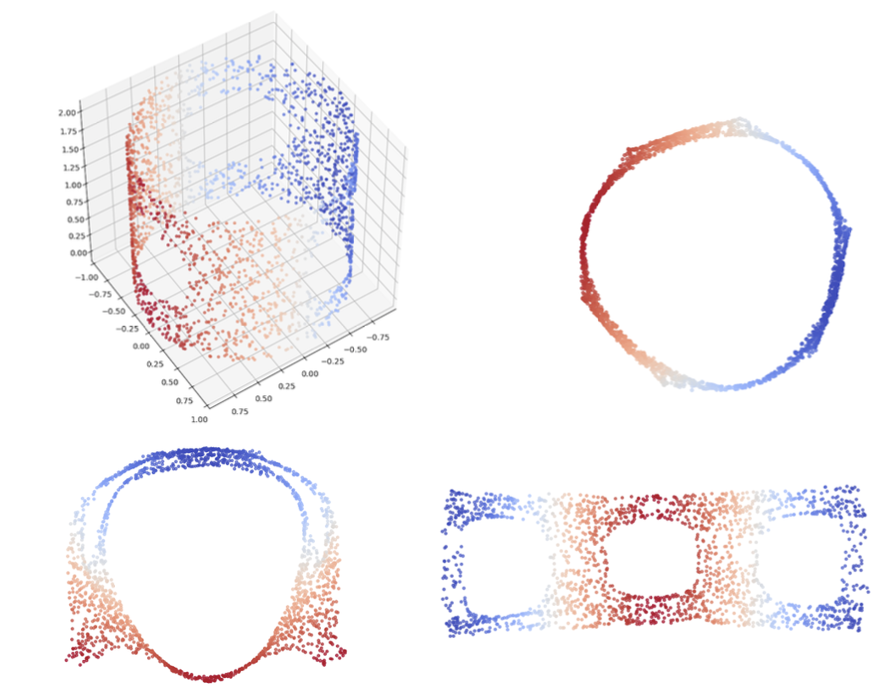
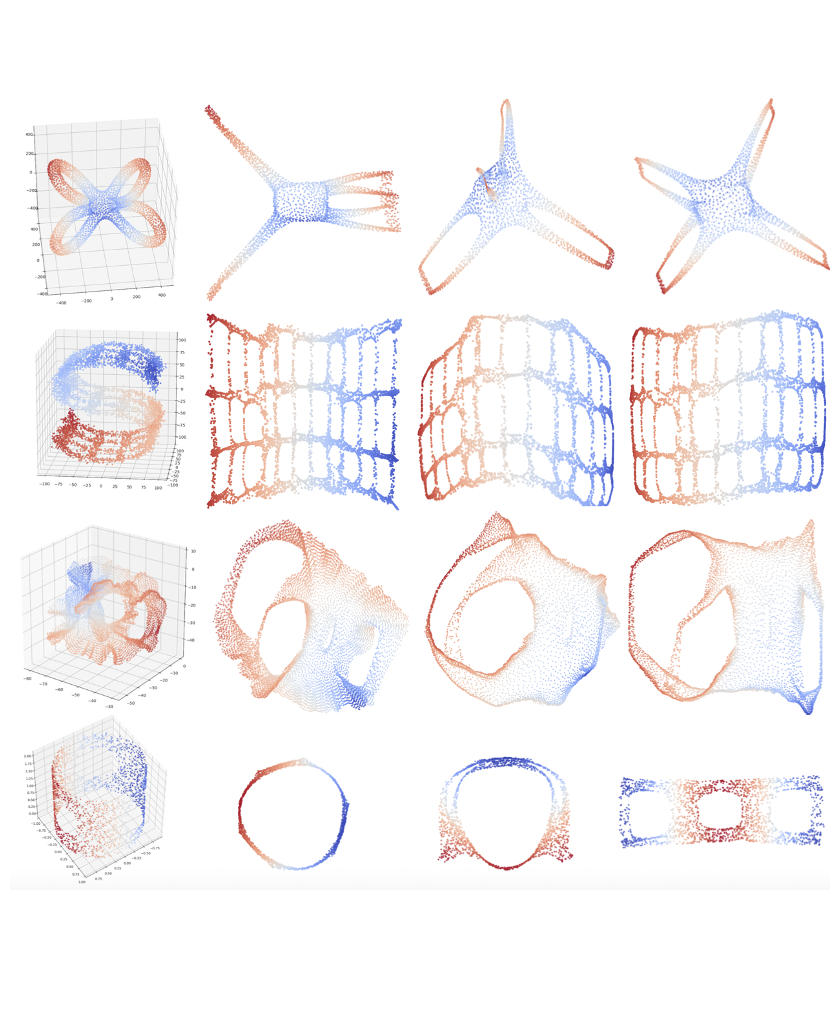
Another example is HIsomap [VDS18], a topology-preserving dimensionality reduction (DR) technique for high-dimensional point clouds. It uses the data skeleton based on the mapper graph, a type of topological descriptor, to select landmarks and integrate these landmarks with the classic DR technique Isomap to preserve topology.

References

2023

2018